Die Beschränktheit und Endlichkeit des Kapitalismus

[...]

Eine einfache Simulation - Ex Pluribus Unum (Aus Vielen Einen)

Zu den wohl einfachsten ökonomischen Simulationen, die man anstellen kann, gehört wohl die folgende, die insgesamt noch einfacher ist, doch Ähnlichkeit, jedenfalls hinreichende Gemeinsamkeit mit Monopoly hat, so dass sich die Eigenschaften des aus den Regeln des Spiels entstehenden Simulationsprozesses im großen Gesellschaftsspiel mit dem Namen Kapitalismus[+] wiederfinden.

Spielregeln (Basisversion)

In dem Modell[+] gibt es Akteure $i$, die (zunächst) alle das gleiche Verhalten aufweisen und über ein jeweiliges Kapital $k_i$ verfügen, das anfangs für alle gleich groß ist. Die Spielregeln sind für alle Akteure des Spiels die gleichen.

Weiter sei ein existenzsicherndes minimales Kapital $k_\text{min}$ definiert, welches in diesem Gesellschaftsspiel nicht unterschritten werden kann, vergleichbar mit einer existenziellen Grundsicherung. Diese Grundsicherung wird im Verlauf der Simulation als ein unterer „Sockel“ oder eine Art „Bodensatz“ erkennbar.

Das Kernelement des Spiels ist die Umverteilung von Kapital durch den Verleih der Grundsicherung überschüssigen Kapitals gegen Zins[+]. Für alle Akteure gilt ein (durch Knöpfe einstellbarer) Zinssatz[+] von $z$, dessen Vorzeichen in der Simulation auch umgekehrt werden kann.

Alle überschüssigen Kapitale oberhalb der Grundsicherung $k_\text{min}$ werden durch Verleih eingesetzt. Durch den Verleih des überschüssigen Kapitals jedes Akteurs $i$ entstehen Zins[+]-Schulden, die zufällig auf alle anderen Akteure $j\ne i$ verteilt werden. In einem Zeitschritt[+] der Simulation (des Spiels) akkumuliert[+] ein Akteur $i$ also nicht nur Zins[+]-Guthaben, die von den anderen $j\ne i$ genommen werden, sondern auch Zins[+]-Schulden, die am verliehenen Kapital der anderen Akteure entstehen und auf den Akteur $i$ umverteilt wurden. Die zufällig bestimmten Umverteilungskoeffizienten für die Umverteilung sind $p_{i,j\ne i}$.

Sinkt in einem Zeitschritt[+] der Simulation in Folge der Umverteilung der Zins[+]-Schulden bei Akteuren $i$ das Kapital $k_i$ unter die Grundsicherung $k_\text{min}$ („Pleite[+]“ oder Bankrott[+]), dann wird die Differenz (Diskrepanz) zwischen $k_i$ und $k_\text{min}$ addiert und durch eine „Entschuldungssteuer” auf das Kapital $\tau$ auf alle Akteure $j\ne i$ mit Kapital oberhalb der Grundsicherung $k_\text{min}$ umgelegt und also mit dem bereits akkumulierten[+] Kapital gewichtet umverteilt.

Der javascript-Quellcode der Simulation befindet sich hier. Für die mathematischen Details verweise ich auf dieses Dokument.

Simulation

Diskussion

Hat man sich nach ein paar Durchläufen mit der Dynamik des Prozesses vertraut gemacht, wird man bemerkt haben, dass er immer auf eine gleiche Art endet: ein einziger Akteur vereint auf sich die anfangs überschüssigen Kapitale aller anderen, während die übrigen ein Kapital $k_\text{min}$ in Höhe der Grundsicherung haben. Welcher der eine Akteur ist, der am Ende alles hat, ist letztlich dem Zufall in der Frühphase der Simulation geschuldet. Wie man erkennen kann, verstärkt der positive Zins[+] (zufällig) bestehende Ungleichgewichte, so dass ein Akteur, der in der Frühphase des Prozesses über ein wenig mehr als alle anderen verfügt, mit hoher und immer höher werdender Wahrscheinlichkeit seine Führungsposition behält. Umgekehrt bewirkt der positive Zins[+], dass Akteure, denen anfangs (zufällig) mehr Schulden zugewiesen wurden, mit immer weiter sinkender Wahrscheinlichkeit aufsteigen bzw. mit immer höher werdender Wahrscheinlichkeit im Gesellschaftsspiel unten bleiben.

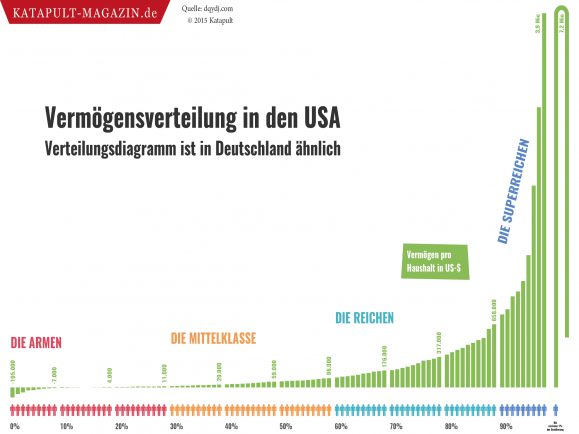
Sortiert man die Verteilung der Kapitale nach der Größe (Knopf »sortieren?«), wobei die größten Kapitale in der Mitte zu finden sind und die kleineren nach links und rechts sortiert bei den Rändern, dann erkennt man eine Pyramidenform, die sich immer weiter zuspitzt, während die Basis der Pyramide immer mehr durch das minimale Kapital $k_\text{min}$ gebildet wird. In der monopolistischen Phase, in der bereits erkennbar ist, welcher Akteur das Spiel gewinnen wird, ist für alle Akteure, die weder das Monopol sind noch den Bodensatz bilden, weil sie nur noch über das minimale Kapital verfügen, also quasi der Mittelstand[+] der simulierten Gesellschaft, klar, dass sie absteigen werden.

In der monopolistischen Phase kann man durch Drücken des Knopfes »Zins[+]-Vorzeichen-Flip« das Vorzeichen des Zinses[+] umkehren. Man sieht dann, dass die Entwicklung genau umgekehrt verläuft wie bei positivem Zins[+]: die größeren Kapitale schmelzen zugunsten der kleineren Kapitale ab und die Verteilung entwickelt sich in Richtung Gleichverteilung. Der Endzustand dieser Negativzins-Ökonomie[+] ist ein dynamisches Gleichgewicht, in der alle zufällig erzeugten Ungleichgewichte abgebaut werden.

Vergleich mit dem zivilisatorischen Gesellschaftsspiel Kapitalismus

Im Gegensatz zur Realität bis an den Anfang des 20. Jahrhundert, in der lange behauptet wurde, dass der nominale Zins[+] nicht unterhalb von 0% gesenkt wird, das sog. zero lower bound (ZLB)-Dogma, kann man an der Simulation alle Möglichkeiten[+] der Geldpolitik[+] studieren. Es handelt sich dabei aber nur um ein Modell[+], dessen Aussagekraft in Bezug auf die Realität aufgrund der Modellannahmen[+] natürlich beschränkt ist. Dennoch gibt es Eigenschaften des Modells[+], die sich aufgrund der Ähnlichkeit der Wirkmechanismen auch in der Realität finden.

Unterschiede

Zunächst einmal kläre ich die expliziten und impliziten Annahmen, die das Modell[+] von der Realität unterscheiden.

• Es fällt auf, dass Arbeit[+] und Konsum, also lebenswesentliche Einnahmen und Ausgaben von Geld nicht berücksichtigt sind. Damit nimmt das Modell[+] implizit an, dass die Akteure wirtschaftlich autark[+] sind, dass sie also mit ihrer Arbeit[+] genau das herstellen, was sie auch konsumieren. Desweiteren arbeiten sie alle gleich viel, bekommen auch alle gleich viel Arbeitslohn[+] und geben alle gleich viel aus, nämlich $k_\text{min}$. Damit ist der kreislaufartige, statische Teil der Wirtschaft (Schumpeter[+]), die Realwirtschaft, in der Simulation ausgeklammert und wird nur als limitierende Größe des Spiels statisch im Spiel erfasst.
• Es gibt nur einen statischen Zins[+], keine Mietzinsen[+], keine Pachtzinsen[+], keine Lizenz-, Nutzungs- und Leihgebühren, also nur eine Art Leihkapital und kein Wachstum[+] der Realwirtschaft. Es wird also nur Finanzwirtschaft, bzw. Geldwirtschaft, Kapitalismus[+] oder Monopoly miteinander gespielt, während für die nackte Existenz gesorgt ist.
• Das Spiel ist ein reines Nullsummenspiel, es wird kein Geld aus dem Nichts geschöpft. Der Zufall bestimmt über die Verteilung von Zinsschulden[+]. In der Realität werden die Sparzinsen über den Staat vom Steuerzahler gezahlt, über die Unternehmen in Form von reduzierten Unternehmens- und Betriebsgewinnen und Inflation[+] und von den Konsumenten über Verbraucherkredite.
• Der Staat verteilt nur über die Entschuldigungssteuer um, ansonsten ist es eine reine Marktwirtschaft[+].
• Implizit nimmt das Modell[+] totale Markttransparenz an. Soziologisch ist dies die Annahme, dass alle Akteure mit allen in Austauschbeziehung stehen. Dies ist eine unrealistische Annahme, denn in realen Wirtschaften werden Beziehungen eine gewisse Regionalität, jedenfalls einen Raumbezug haben. Zwar sind die Märkte des Finanzsystems im Vergleich zu den Märkten der Realwirtschaft transparenter, doch gilt das eben nur für einige Zinsarten[+]. Miet- und Pachtmärkte z.B. haben einen festen Raumbezug.

Wenigstens die hier genannten Unterschiede machen eine Übertragung von Aussagen des Modells[+] auf die Realität in Bezug auf die betreffenden Aspekte unmöglich.

Gemeinsames und Übertragbares

Neben den Unterschieden gibt es Eigenschaften des Modell[+], die seine Aussagen auf die Realität übertragbar machen. Ich beginne dabei zunächst mit der Dynamik des kapitalistischen Prozesses mit positivem Zins[+].

• Was z.B. in Modell[+] und Realität gleich ist, ist die Akkumulationswirkung[+] des Zinsmechanismus[+], die Monopolbildung, und also die Verstärkung der Ungleichgewichte. Die grundlegende Dynamik folgt dem Prinzip, dass die großen die kleinen, überschüssigen Kapitale aufzehren.
• Man beobachtet im Modell[+] den Abbau der Mittelschicht[+]. Alle Kapitale zwischen dem minimalen und dem maximalen Kapital verlieren und gleichen sich immer mehr dem minimalen Kapital an.
• Man erkennt auch, dass eine zufällig enstehende Ungleichheit über die Zeit[+] verstärkt wird. Im mittleren Teil bleiben die relativen Abstände in etwa unverändert.
• Die Verteilung von Zinsschulden[+] auf Kapitale, die nahe bei oder am minimalen Kapital liegen, machen eine soziale Grundsicherung notwendig. Das Sozialstaatsprinzip ist eines der notwendigen Folgen der kapitalistischen Entwicklung. In der Simulation werden Zahlungen, die der Staat zur Absicherung des minimalen Kapitals benötigt, aus den Einnahmen einer Entschuldungssteuer auf Kapital gewonnen. In der Realität gibt es eine solche Steuer auf Vermögen nicht, denn sie stünde im Gegensatz zum Prinzip des Zinses[+], das quasi eine Steuer des Kapitals ist, die jedes Kapital auf alle anderen Kapitale erhebt.
• Man beobachtet die Endlichkeit und den Endzustand des Prozesses (siehe unten). Der Prozess gerät am Ende in eine „Starre”, in der es überhaupt keine Dynamik mehr gibt, weil alle Zinsen[+], die das Monopol nimmt , ihm als Entschuldungssteuer wieder genommen werden. Die einzigen ökonomisch Handelnden sind dann der Staat und das Monopol (Nationalsozialismus).

Bei negativem Zins[+] zeigt die Simulation folgende Dynamik:

• Man beobachtet eine Tendenz in Richtung Angleichung der Kapitale. Entgegen der Intuition[+] der meisten Menschen, die mir in den letzten 5 Jahren begegnet sind, mit denen ich mich über die Wirkung einer Negativzins-Ökonomie[+] unterhalten habe, nehmen insbesondere kleine Kapitale infolge der negativen Zinsen[+] zu. Dies ist ja auch gar nicht verwunderlich, denn es nehmen nur die Kapitale am Spiel Teil, die oberhalb des minimalen Kapitals liegen. Diesen Akteuren in der Grundsicherung wird also gar nichts genommen, weil sie nichts auf's Spiel setzen. Hingegen verlieren die größten Kapitale am meisten. Über den Verteilungsmechanismus wird dieses Kapital zufällig auch und am Ende vor allem auf Akteure verteilt, deren Kapitale minimal sind.
• Man beobachtet wenigstens am Ende eine Gleichheit und Beschränktheit der Kapitale. Die Beschränkheit ist in einem umlaufgesicherten Vollreservesystem[+] nicht allein der Beschränkheit der Geldmenge[+] geschuldet, sondern logische Folge des Negativzinses.

Berechnung der Lebensdauer des kapitalistischen Prozesses

[...] mathematische Details.

Querverweise auf 'Die Beschränktheit und Endlichkeit des Kapitalismus'

• Kommentierung: Thema 'Ungleichheit und Wirtschaftswachstum' bei 'Jung und Naiv' mit Maurice Höfgen, Martyna Linartas, Marcel Fratzscher und Silja Graupe; Diskussion über Erscheinungsformen von Ungleichheit; Wachstumsdiskussion; Fazit
• Widergabe einer E-Mail: Macht und Kontrollbegrenzung; Meine Antwort; Das Märchen von der Selbstregulierung der Märkte im Kapitalismus; Implizite Macht- und Kontrollbegrenzung infolge einer Negativzins-Ökonomie
• Eine kurze Diskussion über die Dynamik der Vermögensverteilung im Kapitalismus mit Ruben Altmann; Fazit
• Paul Kirchhofs YouTube-Beitrag zu den Negativzinsen bei Mission Money; Kommentierung; Geld arbeitet nicht, sondern Geld lässt arbeiten; Leugnung der Gefährdung der Stabilität und des Vertrauens durch Fortsetzung des Zinsnehmens; Falsche Anwendung des Gleichheitsgrundsatzes; Fingierte Bedrohung der Familie, der Freiheit und des Eigentums; Kommt der Crash?; Zur Missachtung der Stabilitätskriterien; Austerität als Lösung; Fazit; Referenzen / Einzelnachweise
• Den Politikern des linken Spektrums fehlt es an ökonomischer Kompetenz; Kommentierung einer Aussage Robert Habecks zum Wahlkampfprogramm der Union; Anschließende Diskussion mit tieferer Begründung; Positionierung innerhalb des ordnungspolitischen Rahmens; Nachträge und Erläuterungen; Welchen Einfluss hat die Kreditaufnahme des Staates normalerweise auf das Zinsniveau im Währungsraum?; Geldpolitik und die Ordinate der Ordnungspolitik; Warum ich glaube, dass das Wahlkampfprogramm der Union implizit die Negativzins-Ökonomie enthält; Lichtblick
• Zusammenfassung einiger makroökonomischer Folgen einer Negativzins-Ökonomie; Entropiezunahme und Negativzins; Altersvorsorge unter einer Negativzins-Ökonomie; Inflation des Gelduniversums, Kontrahierungszwänge und das Gesetz des tendenziellen Falls der Profitrate; Welche Rolle spielen dabei Abschreibungen an realem (Sach-) Kapital? Vermögensbegrenzung; Das Vorzeichen der Inflationsrate und das Zinsvorzeichen
• Auseinandersetzung mit Kritik und Hinterfragungen; Ursprungstext; Zum Realismus der Monopoly-Simulation; Das geltende Tote und der Zins-Mechanismus: einfache Ursache, hochkomplexe Wirkung; Warum denken nicht mehr Wissenschaftler und andere Denkfähige über den Zins-Mechanismus nach?; Grausamkeit der Zivilisation gegenüber der Grausamkeit in Ökosystemen; Fortsetzung; Präzisierung des Begriffs des 'geltenden Toten' und Motiv seiner Verwendung; Die klaffende, zentrale Bildungslücke rund um Geld, Zins und Kapitalismus und Anzeichen einer Verschwörung
• Kommentierung eines Videos eines Geldsystem-Crash-Propheten; Das Gejammer einstellen und verantwortungsvoll handeln; Der Klassiker: manipulierte Märkte; Autonomie und Heteronomie der Zentralbank gegenüber den Marktprozessen; Negativzins als Vermögenssteuer
• Aus einer Unterhaltung über die Entwicklung der Selbstständigenquote unter einer Negativzins-Ökonomie; Wo bleibt die Inflation? Ein Podcast von einem Mitglied der europäischen Zentralbank über die Kaufkraftentwicklung von feststehenden Einkommen und Geldbeträgen.; Ist die Corona Pandemie eine vorsätzlich herbeigeführte Störung, die zum Anlass genommen wird eine autoritäre Ordnung zu errichten?
• Unwissenheitsmanagement: Kapitalismus, Intuition und Konflikt; Überall falsche Propheten, Unkrautsäer und babylonische Sprachverwirrung; Wie sich Intuition bildet; Der Rahmen der Weltanschauung und -erfahrung; Kapitalistische Sozialisation; Projektion auf der Grundlage des inneren Weltmodells; Durch das Kapital und seine Fortpflanzung bedingte soziale Kausalität; Der Systemanteil im Selbst; Zwei Klassen und zwei Wahrheiten; Das Rechts-Links-Schema; Schluss mit der Spalterei und dem blinden, unhinterfragten Gehorsam den eigenen Affekten gegenüber!; Negative Zinsen, wer weiß schon, wie das geht?; Viele der neuen Freiheiten und Wandlungsmöglichkeiten liegen in einer bestimmten Richtung. Welche Richtung ist das und wer bestimmt, welche Freiheiten sinnvoll sind?
• Beschreibung der spätkapitalistischen Verwertungskrise des Kapitals nach Alfred Sohn-Rethel; Kommentierung von Kapitel 3: Das Dilemma der Rationalisierung; Erweiterung des reproduktiven Lebensraums des Kapitals: Globalisierung; Zusammensetzung der Fixkosten; Folge einer Negativzins-Ökonomie: Absenken der Fixkosten durch Vergemeinschaftung des Produktionskapitals
• Wie koordiniert man den Schwarm?; Sequentielle oder parallele Führung?; Zentralverwaltungswirtschaft vs. Marktwirtschaft; Zusammenspiel von Geld-, Finanz- und Fiskalpolitik; Warum verteidigen gerade kapitalophile politische Fraktionen die schwarze Null?; Prozessmusterumkehr infolge der Umkehr des Vorzeichens bei den nominalen Geldzinsen; Implikationen und Möglichkeiten für Finanz- und Ordnungspolitik; Worin bestehen die Herausforderungen?
• Ein Lehrstück der „Ökonomie-Verschwurbelung“ der AfD, und wie man die systematische Gehirnwäsche entlarvt; Analyse; Fazit
• Zwei Ergebnisse kapitalistischer Erziehung: Wissen und Verhaltenanpassungen; Kontingentes in unterschiedlichen Darstellungen; Simmel zu Objektivität, objektiver Geist, Wahrheit, Erkenntnis und Notwendigkeiten; Über-Ich und Es, Intellekt und Affekt, Seele und Leib, objektiver und subjektiver Geist; Zusammenfassung
• Monopoly-Simulation
• Negativzinswirtschaft; Ursachen, Entstehung und Verlauf; Juli 2015; Ursachen der Entstehung; Auswirkungen des Zinsvorzeichenwechsels; Maßnahmen an der Null-Zins-Grenze; Grundrechte; Zeitentwicklung von Vermögen; Einfluss auf das Sozialverhalten; Referenzen / Einzelnachweise
• Einkopplung in das Geld-Netzwerk; Das Geld-Netzwerk; Vertragsarten, Austauschformen und Erwerbsklassen; Zuordnung von Eigentums und Besitzgütern, Eigentums und Besitzverhältnisse oder Güterbeziehungen; Vertragsarten; Einteilung in Geld- und Güter-Erwerbsklassen; Formen der Bestimmung im Vertrags- und Gesetzesraum; Bürger und Staat; Mengen im Vertrags- und Gesetzesraum: Ökonomie, Politik, Wirtschaft, Handel, Arbeit und Dienstleistung; Kopplung psychischer und sozialer System: Subjektive, Konsensuale und Oktroyierte Bewertungen; Zins, Verhalten und Bewertung; Referenzen / Einzelnachweise
• Räume monetärer Möglichkeiten und die Verteilung des Vermögens, individuelle Budgets; Weintrauben und Weinbeeren; Die Vermögensverteilung und die zwei Klassen im Kapitalismus; Einfluss der Geldzinsen; Auf- und Abstieg: Sparen und die Kredithürde als Schranke zur selbstständigen Existenz
• Die faschistisch organisierten Eigentums- und Machtverhältnisse im Kapitalismus; Terminologie für Organisationsformen und Definition des Faschismus; Harmonie; Rang; Schuld und Zwang; Faszination; Die Zinssekte, der theo-ökonomische Komplex und seine Evolution; Das kapitalistische Wertsystem, sein Darwinismus und seine Übertragung; Prinzipien der Wertung, der Ungleichwertigkeit und der Wertung des Selbst; Machtmittel in der Verzerrung des Gleichgewichts der Bestimmung; Das Phänomen des Faschismus im Europa des 20. Jahrhunderts; Referenzen / Einzelnachweise
• Wirkung des Kapitalismus auf die Umwelt; Wirtschaft als Netzwerk von Austauschbeziehungen; Ungestörte Austauschbeziehungen - freie Märkte; Gestörte Austauschbeziehungen als Folgewirkung des Zinses; Die Organe der menschenlichen Produktionsmatrix: Unternehmen und Lieferketten; Kritik des positiven Zinses im Mittel-Zweck-Schema im Hinblick auf die ökologischen und sozialen Schäden; Suggestiv überhöhte Zwecke: Konsumpropaganda; Suggestive Minderung des Wertes des Mittels; Verdrängung und Ignoranz; Ist der Urzins noch zu retten?; Referenzen / Einzelnachweise